Depth Without the Magic

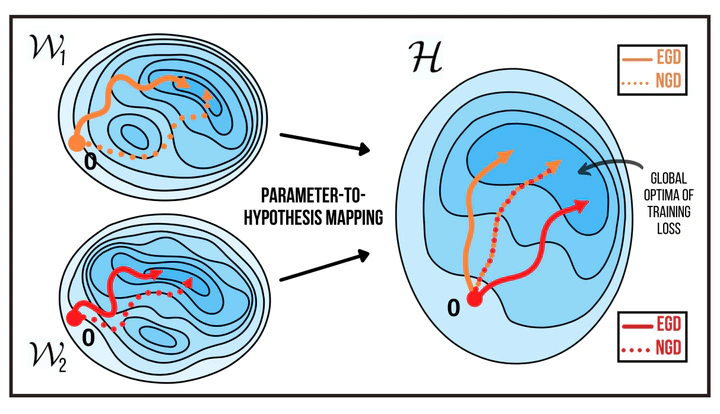
In gradient descent, changing how we parametrize the model can lead to drastically different optimization trajectories. This gives rise to a surprising range of meaningful inductive biases: identifying sparse classifiers or reconstructing low-rank matrices without explicit regularization. This implicit regularization has been hypothesized to be a contributing factor to good generalization in deep learning. However, natural gradient descent is approximately invariant to reparameterization, it always follows the same trajectory and finds the same optimum. The question naturally arises: What happens if we eliminate the role of parameterization, which solution will be found, and what new properties occur? We characterize the behavior of natural gradient flow in deep linear networks for separable classification under logistic loss and deep matrix factorization. Some of our findings extend to nonlinear neural networks with sufficient but finite over-parametrization. We demonstrate that there exist learning problems where natural gradient descent fails to generalize, while gradient descent with the right architecture performs well.